Estimation Methods – catsim.estimation

Estimators are the objects responsible for estimating examinees’ ability values, given a dichotomous (binary) response vector and an array of the items answered by the examinee. In the domain of IRT, there are two main types of methods for estimating \(\hat{\theta}\): Bayesian methods and maximum-likelihood methods.

Maximum-likelihood methods choose the \(\hat{\theta}\) value that maximizes the likelihood (see catsim.irt.log_likelihood()) of an examinee having a certain response vector, given the corresponding item parameters.

Bayesian methods use a priori information (usually assuming ability and parameter distributions) to make new estimations. New estimations are then used to refine assumptions about the parameter distributions, improving future estimations.

All implemented classes in this module inherit from a base abstract class BaseEstimator. Simulator allows that a custom estimator be used during the simulation, as long as it also inherits from BaseEstimator.

catsim implements a few types of maximum-likelihood estimators.

Ability estimation components for CAT.

class catsim.estimation.BaseEstimator(verbose: bool = False)

Bases: Simulable, ABC

Base class for ability estimators.

Estimators are responsible for computing ability estimates based on examinees’ responses to administered items.

Parameters:

verbosebool, optional

Whether to be verbose during execution. Default is False.

property avg_evaluations: float

Get the average number of function evaluations for all tests the estimator has been used.

Returns:

float

Average number of function evaluations per test.

property calls: int

Get how many times the estimator has been called to maximize/minimize the log-likelihood function.

Returns:

int

Number of times the estimator has been called to maximize/minimize the log-likelihood function.

abstractmethod estimate(index: int | None = None, item_bank: ItemBank | None = None, administered_items: list[int] | None = None, response_vector: list[bool] | None = None, est_theta: float | None = None) → float

Compute the theta value that maximizes the log-likelihood function for the given examinee.

When this method is used inside a simulator, its arguments are automatically filled. Outside of a simulation, the user can also specify the arguments to use the Estimator as a standalone object.

Parameters:

indexint or None, optional

Index of the current examinee in the simulator. Default is None.

item_bankItemBank or None, optional

An ItemBank containing item parameters. Default is None.

administered_itemslist[int] or None, optional

A list containing the indexes of items that were already administered. Default is None.

response_vectorlist[bool] or None, optional

A boolean list containing the examinee’s answers to the administered items. Default is None.

est_thetafloat or None, optional

A float containing the current estimated ability. Default is None.

Returns:

float

The current estimated ability \(\hat\theta\).

property evaluations: int

Get the total number of times the estimator has evaluated the log-likelihood function during its existence.

Returns:

int

Number of function evaluations.

class catsim.estimation.NumericalSearchEstimator(tol: float = 1e-06, dodd: bool = True, verbose: bool = False, method: str = 'bounded')

Bases: BaseEstimator

Implement search algorithms in unimodal functions to find the maximum of the log-likelihood function.

This class provides multiple numerical search methods for ability estimation in IRT, including ternary search, dichotomous search, Fibonacci search, and golden-section search, according to [Veliz20]. Also check [Brent02]. It is also possible to use the methods from scipy.optimize.minimize_scalar().

Parameters:

tolfloat, optional

Tolerance for convergence in the optimization algorithm. Default is 1e-6.

doddbool, optional

Whether to employ Dodd’s estimation heuristic [Dod90] when the response vector only has one kind of response (all correct or all incorrect, see catsim.cat.dodd()). Default is True.

verbosebool, optional

Whether to print detailed information during optimization. Default is False.

methodstr, optional

The search method to employ. Must be one of: ‘ternary’, ‘dichotomous’, ‘fibonacci’, ‘golden’, ‘brent’, ‘bounded’, or ‘golden2’. Default is ‘bounded’.

static available_methods() → frozenset[str]

Get a set of available estimation methods.

Returns:

frozenset[str]

Set of available estimation methods: {‘ternary’, ‘dichotomous’, ‘fibonacci’, ‘golden’, ‘brent’, ‘bounded’, ‘golden2’}.

property dodd: bool

Whether Dodd’s estimation heuristic [Dod90] will be used by the estimator.

Dodd’s method is used when the response vector is composed solely of correct or incorrect answers, to prevent maximum likelihood methods from returning -infinity or +infinity.

Returns:

bool

Boolean value indicating if Dodd’s method will be used or not.

See also

catsim.cat.dodd

Implementation of Dodd’s estimation heuristic.

estimate(index: int | None = None, item_bank: ItemBank | None = None, administered_items: list[int] | None = None, response_vector: list[bool] | None = None, est_theta: float | None = None) → float

Compute the theta value that maximizes the log-likelihood function for the given examinee.

When this method is used inside a simulator, its arguments are automatically filled. Outside of a simulation, the user can also specify the arguments to use the Estimator as a standalone object.

Parameters:

indexint or None, optional

Index of the current examinee in the simulator. Default is None.

item_bankItemBank or None, optional

An ItemBank containing item parameters. Default is None.

administered_itemslist[int] or None, optional

A list containing the indexes of items that were already administered. Default is None.

response_vectorlist[bool] or None, optional

A boolean list containing the examinee’s answers to the administered items. Default is None.

est_thetafloat or None, optional

A float containing the current estimated ability. Default is None.

Returns:

float

The current estimated ability \(\hat\theta\).

Raises:

ValueError

If required parameters are None when not using a simulator.

property method: str

Get the estimator search method selected during instantiation.

Returns:

str

The search method (‘ternary’, ‘dichotomous’, ‘fibonacci’, ‘golden’, ‘brent’, ‘bounded’, or ‘golden2’).

Comparison between estimators

The chart below displays the execution times of the same simulation (100 examinees, an item bank of 300 questions and 20 items per test) using different \(\hat{\theta}\) estimation methods.

(Source code, png, hires.png, pdf)

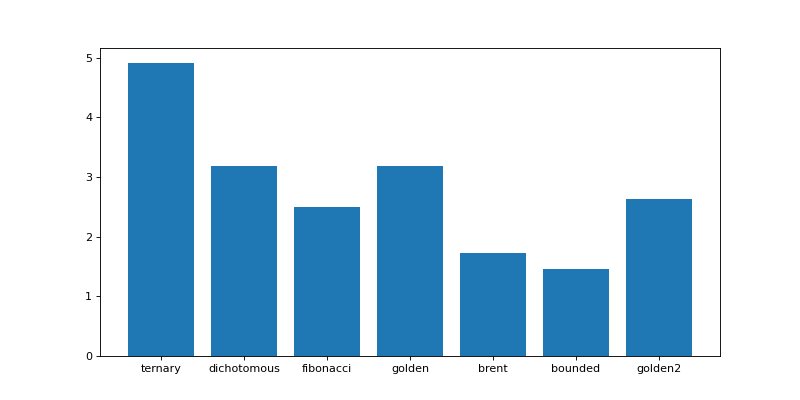
Fig. 3 Execution times of the same simulation (100 examinees, an item bank of 300 questions and 20 items per test) using different \(\hat{\theta}\) estimation methods.

The charts below show the \(\hat{\theta}\) found by the different estimation methods, given three dichotomous response vectors with different numbers of correct answers. All estimators reach comparable results, maximizing the log-likelihood function. The main difference among them is in the number of calls to catsim.irt.log_likelihood(). Methods that require less calls to maximize the function are usually more time efficient.

(Source code, png, hires.png, pdf)

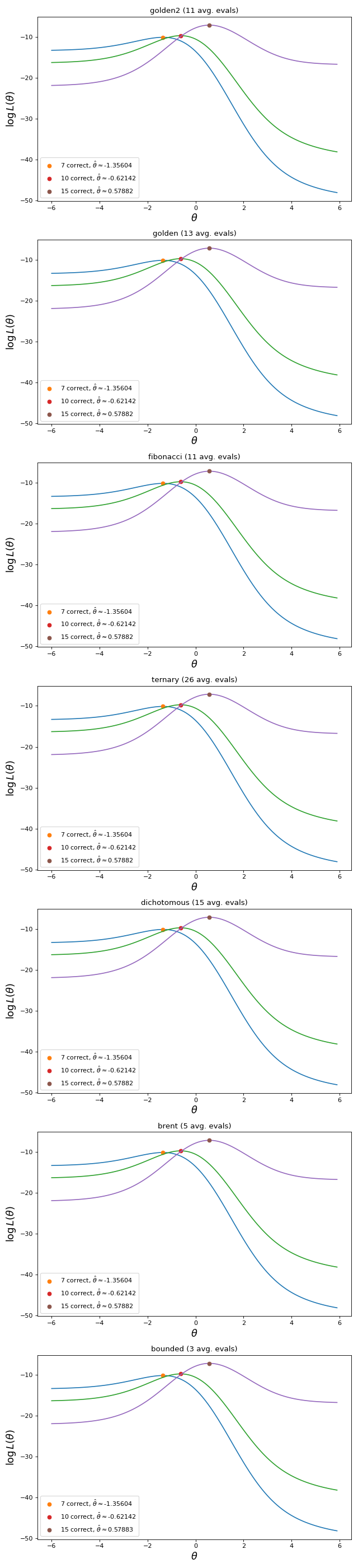
Fig. 5 \(\hat{\theta}\) found by the different estimation methods, given three dichotomous response vectors with different numbers of correct answers. All estimators reach comparable results, maximizing the log-likelihood function.