Classificação da base de dados Iris - redes menores e regularização
Introdução
Este notebook continua uma série na qual foram introduzidas a base de dados Iris e o método de treinamento e avaliação de redes neurais [1] e o PCA [2].
No primeiro notebook, foram mencionadas duas coisas que serão testadas aqui.
- redes neurais maiores (com mais pesos treináveis) possuem maior predisposição ao overfitting.
- existe uma técnica, chamada regularização, capaz de combater o overfitting.
Neste notebook, uma rede consideravelmente menor será treinada para classificar a base de dados Iris. Não só isso, como ela usará a primeira componente principal retornada pelo PCA, trabalhando tanto com menos pesos como menos dados.
Além disso, treinaremos a rede neural original, utilizada nos notebooks anteriores, com regularização L2 e observaremos a ausência de overfitting quando a rede é treinada por longos períodos de tempo.
Importando pacotes e criando funções
As funções abaixo aplicam o PCA numa base de dados e avaliam uma rede neural, retornando as medidas para serem exibidas em gráficos posteriormente.
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import tensorflow.keras as keras
import numpy as np
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
def apply_PCA(X, n_components):
pca = PCA(n_components=n_components)
new_X = pca.fit_transform(iris_X)
print('Tamanho da base de dados antes: ', X.shape)
print('Tamanho da base de dados depois: ', new_X.shape)
print('Porcentagem da variância explicada por cada coluna:', pca.explained_variance_ratio_)
print('Variância acumulada nas colunas remanescentes:', sum(pca.explained_variance_ratio_))
return new_X
def evaluate_model(model, X, y):
X_train, X_test, y_train, y_test = train_test_split(X,
y,
test_size = 0.2,
random_state=123)
y_train_onehot = keras.utils.to_categorical(y_train, num_classes = 3)
y_test_onehot = keras.utils.to_categorical(y_test, num_classes = 3)
model.save_weights('weights.hdf5')
history = model.fit(X_train, y_train_onehot, validation_split=.1, epochs=2500, verbose=0)
y_pred = model.predict(X_test)
y_pred_onehot = y_pred.argmax(axis=1)
print(classification_report(y_test, y_pred_onehot))
v1 = history.history['categorical_accuracy']
v2 = history.history['loss']
v3 = history.history['val_categorical_accuracy']
v4 = history.history['val_loss']
model.load_weights('weights.hdf5')
history = model.fit(X_train, y_train_onehot, epochs=150, verbose=0)
v5 = history.history['categorical_accuracy']
v6 = history.history['loss']
y_pred = model.predict(X_test)
y_pred_onehot = y_pred.argmax(axis=1)
print(classification_report(y_test, y_pred_onehot))
return v1, v2, v3, v4, v5, v6
Preparando os dados
Usaremos o pacote scikit-learn para carregar a base de dados Iris. Vamos geraruma versão da base com o menor número possível de componentes principais (1).
iris_X, iris_y = load_iris(return_X_y=True)
iris_X_tiny = apply_PCA(iris_X, 1)
Tamanho da base de dados antes: (150, 4)
Tamanho da base de dados depois: (150, 1)
Porcentagem da variância explicada por cada coluna: [0.92461872]
Variância acumulada nas colunas remanescentes: 0.9246187232017271
Regularização
Em termos matemáticos, o overfitting ocorre quando os pesos de uma rede neural assumem magnitudes (positivas ou negativas) muito altas, permitindo que as funções que essas redes neurais modelam se tornem demasiadamente complexas para a função de erro que tentam minimizar.
Na imagem abaixo, ambas as funções azul e verde se ajustam aos dados vermelhos, porém a função azul assumiu uma forma desnecessariamente complexa. Caso um novo ponto vermelho seja adicionado, é possível que a função verde esteja mais próxima dele do que a função azul, indicando que a função verde generaliza melhor os dados observados, mesmo sendo mais simples.
A diferença entre as duas funções está no fato da função verde ter sido regularizada. Em sua forma mais simples, a regularização é feita somando-se os pesos da rede neural à função de erro que a rede tenta minimizar. Imaginando que \(L(\theta)\) é a função de erro que usamos até agora, \(R(\theta)\) é o novo termo de regularização que incluímos.
\[J(\theta)=L(\theta) + \lambda R(\theta)\]
Uma regularização comumente usada é a L2, na qual somamos o quadrado dos pesos da rede neural à função de erro. Isso tem o efeito de punir demasiadamente pesos muito grandes, ignorando pesos pequenos. O termo \(\lambda\) é um coeficiente que indica o quão relevante o termo de regularização é na fórmula total do erro. Ele será utilizado na declaração da rede neural que faremos em Keras.
\[J(\theta)=L(\theta) + \lambda \sum_w^{\theta}w^2\]
Com a regularização, a rede neural deve alcançar o menor erro possível com os menores pesos possíveis, evitando o overfitting.
As funções abaixo vão criar as rede neurais.
- A primeira foi utilizada nos tutoriais anterior e possui 4 entradas, 4 camadas e 213 pesos treináveis.
- A segunda é igual à primeira, porém com a regularização configurada nas camadas.
- A última rede possui aproximadamente 10% do tamanho da primeira, 1 entrada, 3 camadas e 23 pesos treináveis.
def create_large_model(input_dim):
model = Sequential()
model.add(Dense(10, activation='tanh', input_dim=input_dim))
model.add(Dense(8,activation='tanh'))
model.add(Dense(6,activation='tanh'))
model.add(Dense(3,activation='softmax'))
model.compile('adam','categorical_crossentropy', metrics=['categorical_accuracy'])
return model
def create_regularized_model(input_dim):
model = Sequential()
model.add(Dense(10, activation='tanh', kernel_regularizer='l2', bias_regularizer='l2', input_dim=input_dim))
model.add(Dense(8,activation='tanh', kernel_regularizer='l2', bias_regularizer='l2'))
model.add(Dense(6,activation='tanh', kernel_regularizer='l2', bias_regularizer='l2'))
model.add(Dense(3,activation='softmax', kernel_regularizer='l2', bias_regularizer='l2'))
model.compile('adam','categorical_crossentropy', metrics=['categorical_accuracy'])
return model
def create_tiny_model(input_dim):
model = Sequential()
model.add(Dense(3, activation='tanh', input_dim=input_dim))
model.add(Dense(2,activation='tanh'))
model.add(Dense(3,activation='softmax'))
model.compile('adam','categorical_crossentropy', metrics=['categorical_accuracy'])
return model
large_net = create_large_model(iris_X.shape[1])
reg_net = create_regularized_model(iris_X.shape[1])
tiny_net = create_tiny_model(iris_X_tiny.shape[1])
large_net.summary()
tiny_net.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 10) 50
_________________________________________________________________
dense_1 (Dense) (None, 8) 88
_________________________________________________________________
dense_2 (Dense) (None, 6) 54
_________________________________________________________________
dense_3 (Dense) (None, 3) 21
=================================================================
Total params: 213
Trainable params: 213
Non-trainable params: 0
_________________________________________________________________
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_8 (Dense) (None, 3) 6
_________________________________________________________________
dense_9 (Dense) (None, 2) 8
_________________________________________________________________
dense_10 (Dense) (None, 3) 9
=================================================================
Total params: 23
Trainable params: 23
Non-trainable params: 0
_________________________________________________________________
Vamos utilizar nossa função evaluate_model() para avaliar as redes. As redes maiorws serão treinadas na base original e a rede menor, na 1ª componente principal dessa base.
acc1_large, l1_large, acc_v_large, lv_large, acc2_large, l2_large = evaluate_model(large_net, iris_X, iris_y)
acc1_reg, l1_reg, acc_v_reg, lv_reg, acc2_reg, l2_reg = evaluate_model(reg_net, iris_X, iris_y)
acc1_tiny, l1_tiny, acc_v_tiny, lv_tiny, acc2_tiny, l2_tiny = evaluate_model(tiny_net, iris_X_tiny, iris_y)
precision recall f1-score support
0 1.00 1.00 1.00 13
1 0.75 1.00 0.86 6
2 1.00 0.82 0.90 11
accuracy 0.93 30
macro avg 0.92 0.94 0.92 30
weighted avg 0.95 0.93 0.93 30
precision recall f1-score support
0 1.00 1.00 1.00 13
1 1.00 0.83 0.91 6
2 0.92 1.00 0.96 11
accuracy 0.97 30
macro avg 0.97 0.94 0.96 30
weighted avg 0.97 0.97 0.97 30
precision recall f1-score support
0 1.00 1.00 1.00 13
1 1.00 0.83 0.91 6
2 0.92 1.00 0.96 11
accuracy 0.97 30
macro avg 0.97 0.94 0.96 30
weighted avg 0.97 0.97 0.97 30
precision recall f1-score support
0 1.00 1.00 1.00 13
1 1.00 0.83 0.91 6
2 0.92 1.00 0.96 11
accuracy 0.97 30
macro avg 0.97 0.94 0.96 30
weighted avg 0.97 0.97 0.97 30
precision recall f1-score support
0 1.00 1.00 1.00 13
1 0.67 1.00 0.80 6
2 1.00 0.73 0.84 11
accuracy 0.90 30
macro avg 0.89 0.91 0.88 30
weighted avg 0.93 0.90 0.90 30
precision recall f1-score support
0 1.00 1.00 1.00 13
1 0.83 0.83 0.83 6
2 0.91 0.91 0.91 11
accuracy 0.93 30
macro avg 0.91 0.91 0.91 30
weighted avg 0.93 0.93 0.93 30
São exibidos os valores para cada rede treinada na base de treinamento por 2500 épocas e depois por 150 eṕocas. Espera-se que o desempenho das redes neurais que sofram de overfitting seja inferior nos valores impresso primeiro.
Os valores podem mudar aleatoriamente, porém é possível perceber através dos valores de precisão, recall, F1-score e pela matriz de confusão que o desempenho de ambas as redes é comparável e, muitas vezes, idêntico.
Vamos gerar gráficos das 6 medidas coletadas dos dois modelos.
fig, axes = plt.subplots(3,2, False,figsize=(20, 15), squeeze=True)
axes[0][0].plot(acc1_large)
axes[0][0].plot(acc1_reg)
axes[0][0].plot(acc1_tiny)
axes[0][0].set_title('Acurácia Treino')
axes[0][1].plot(l1_large)
axes[0][1].plot(l1_reg)
axes[0][1].plot(l1_tiny)
axes[0][1].set_title('Erro Treino')
axes[1][0].plot(acc_v_large)
axes[1][0].plot(acc_v_reg)
axes[1][0].plot(acc_v_tiny)
axes[1][0].set_title('Acurácia Val.')
axes[1][1].plot(lv_large)
axes[1][1].plot(lv_reg)
axes[1][1].plot(lv_tiny)
axes[1][1].set_title('Erro Val.')
axes[2][0].plot(acc2_large)
axes[2][0].plot(acc2_reg)
axes[2][0].plot(acc2_tiny)
axes[2][0].set_title('Acurácia total')
axes[2][1].plot(l2_large)
axes[2][1].plot(l2_reg)
axes[2][1].plot(l2_tiny)
axes[2][1].set_title('Erro total')
legenda = ['Grande', 'Regularizada', 'Pequena']
xlabel = 'Épocas'
axes[0][0].legend(legenda)
axes[1][0].legend(legenda)
axes[2][0].legend(legenda)
axes[0][1].legend(legenda)
axes[1][1].legend(legenda)
axes[2][1].legend(legenda)
axes[0][0].set_xlabel(xlabel)
axes[1][0].set_xlabel(xlabel)
axes[2][0].set_xlabel(xlabel)
axes[0][1].set_xlabel(xlabel)
axes[1][1].set_xlabel(xlabel)
axes[2][1].set_xlabel(xlabel)
plt.show()
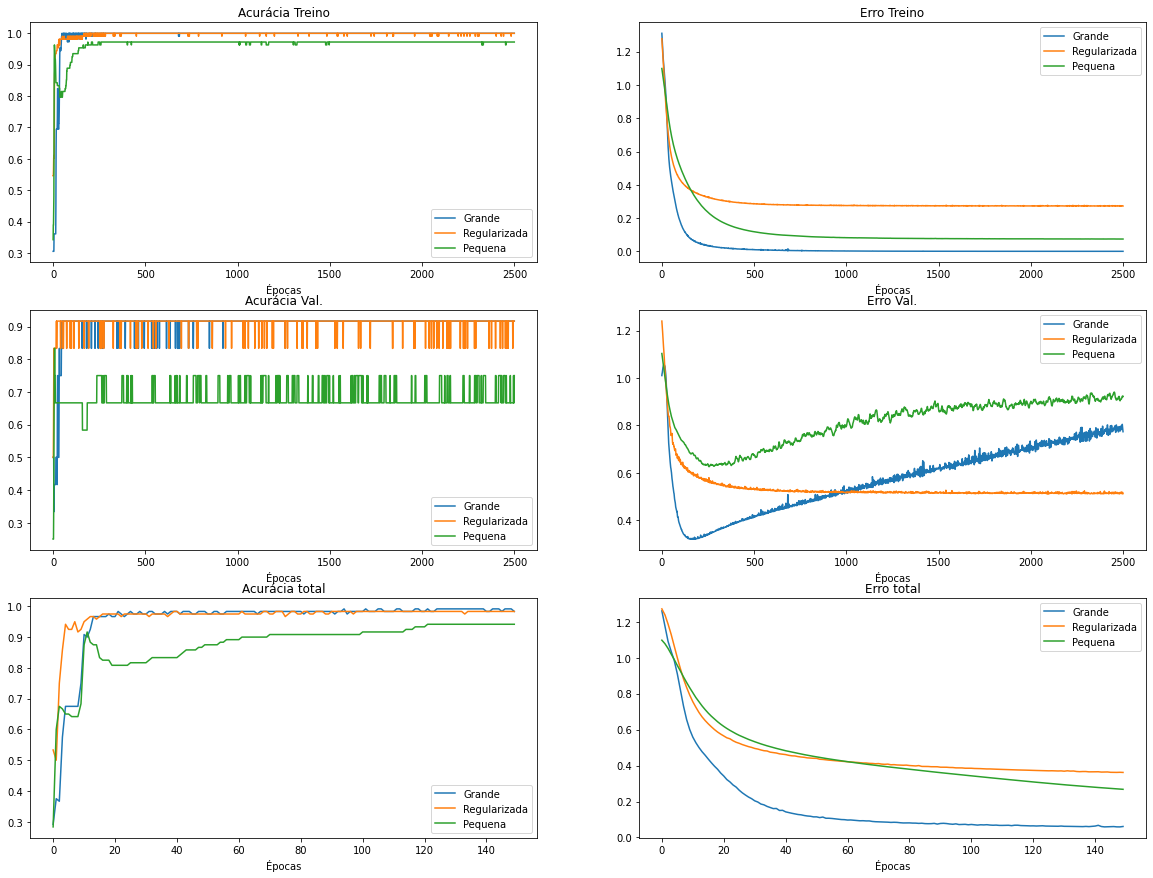
Ambas as redes foram treinadas por 2500 épocas e avaliadas no conjunto de validação para constatar a presença de overfitting (4 primeiros gráficos). Depois, foram treinadas novamente por 150 épocas na totalidade dos dados de treinamento (2 últimos gráficos).
O gráfico de erro no conjunto de treinamento (topo, direita) nos mostra que a rede menor leva mais épocas para aprender. Seu erro diminui lentamente. A rede regularizada não consegue diminuir seu erro tanto quanto as redes não regularizadas devido à restrição em seus pesos. Isso pode parecer ruim, mas veremos um efeito positivo da regularização a seguir.
O gráfico de erro no conjunto de validação (centro, direita) demonstra que o erro da rede grande não-regularizada começa a crescer linearmente após aproximadamente 200 épocas. Um período de treinamento muito extenso apenas prejudica esta rede. A rede menor, apesar de ser menos afetada pelo overfitting, ainda demonstra aumenta do erro após muitas épocas de treinamento. Porém, este aumento é mais lento que na rede neural grande. Por último, a rede grande regularizada não demonstra aumento do erro no conjunto de validação, independente da quantidade de épocas de treinamento.
Essa é uma característica interessante no mundo real, quando não sabemos exatamente a topologia exata da rede neural que solucionará nosso problema em questão, ou por quantas épocas de treinamento é necessário treinar o modelo.
Conclusão
Este notebook demonstrou que uma rede neural consideravelmente menor que a utilizada até o momento é capaz de realizar a classificação das flores na base de dados Iris, utilizando 1/4 dos valores de entrada, 3/4 do número de camadas e aproximadamente 1/10 dos pesos treináveis.
Enjoy Reading This Article?
Here are some more articles you might like to read next: