Classificação da base de dados Iris utilizando redes neurais e PCA
Introdução
Este notebook exemplifica a redução de dimensionalidades de uma base de dados e a posterior classificação de seus itens utilizando uma rede neural. A redução de dimensionalidades é executada utilizando análise de componentes principais, disponível no pacote scikit-learn e a rede neural é um perceptron multi-camadas, construído utilizando Keras.
Este notebook é uma continuação de um outro no qual a base de dados utilizada (Iris) e o método de treinamento e avaliação da rede neural já foram descritos. O notebook anterior está disponível aqui.
Importando pacotes e criando funções
Vamos utilizar scikit-learn e Keras. Também vamos criar algumas funções para simplificar o treinamento e avaliar de uma rede neural, que já foram descritos no notebook anterior.
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import tensorflow.keras as keras
import numpy as np
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
def create_model(input_dim):
model = Sequential()
model.add(Dense(10, activation='tanh', input_dim=input_dim))
model.add(Dense(8,activation='tanh'))
model.add(Dense(6,activation='tanh'))
model.add(Dense(3,activation='softmax'))
model.compile('adam','categorical_crossentropy', metrics=['categorical_accuracy'])
return model
def plot_metrics(history):
fig, axes = plt.subplots(2,1, True,figsize=(8,12))
# "Accuracy"
axes[0].plot(history.history['categorical_accuracy'])
axes[0].set_title('Acurácia')
# "Loss"
axes[1].plot(history.history['loss'])
axes[1].set_title('Erro')
if 'val_loss' in history.history.keys():
axes[0].plot(history.history['val_categorical_accuracy'])
axes[1].plot(history.history['val_loss'])
axes[0].legend(['Treino', 'Validação'])
axes[1].legend(['Treino', 'Validação'])
plt.xlabel('Épocas')
plt.show()
def do_everything(X, y):
X_train, X_test, y_train, y_test = train_test_split(X,
y,
test_size = 0.2,
random_state=123)
y_train_onehot = keras.utils.to_categorical(y_train, num_classes = 3)
y_test_onehot = keras.utils.to_categorical(y_test, num_classes = 3)
model=create_model(X.shape[1])
print(model.summary())
history = model.fit(X_train, y_train_onehot, validation_split=.1, epochs=500, verbose=0)
plot_metrics(history)
model=create_model(X.shape[1])
history = model.fit(X_train, y_train_onehot, epochs=150, verbose=0)
plot_metrics(history)
y_pred = model.predict(X_test)
y_pred_onehot = y_pred.argmax(axis=1)
print(classification_report(y_test, y_pred_onehot))
print(confusion_matrix(y_test, y_pred_onehot))
Análise de componentes principais
A análise de componentes principais (PCA, do inglês principal component analysis) é uma técnica matemática que detecta correlações nas colunas de uma matriz \(X\) e realiza uma transformação linear em \(X\) de forma a reduzir tais correlações.
Em linhas gerais, dados altamente correlacionadas são pouco informativos, inclusive para o treinamento de um classificador. Considere uma base de dados hipotética de cidades que possui as seguintes informações para cada cidade:
- distância do Equador em quilômetros
- distância do Equador em léguas
- temperatura em °C
- temperatura em °F
É possível perceber que os dados 1 e 2 são redundantes, por armazenarem a mesma informação, apenas em escalas diferentes, assim como os dados 3 e 4. Não só isso, como a temperatura de uma cidade é altamente correlacionada com sua distância do Equador. Uma técnica como o PCA encontraria as correlações nesta matriz de 4 colunas e transformaria as colunas de forma a reduzir (ou zerar) tais correlações.
Esta transformação pode ter como efeito colateral a concentração da informação das colunas na matriz original em menos colunas na matriz transformada. Por consequência, seria possível remover as colunas menos informativas, reduzindo a complexidade dos dados, mas retendo a informação necessária para se treinar um classificador, por exemplo.
A redução de dimensionalidade de dados proveniente do PCA também é útil para fins de visualização de dados multidimensionais.
Preparando os dados
Usaremos o pacote scikit-learn para carregar a base de dados Iris. Repare que ela possui 150 flores e 4 características por flor. No notebook anterior, utilizamos todas as 4 características para treinar nossa rede neural. Neste notebook, tentaremos realizar a mesma classificação com um menor número de características.
iris_X, iris_y = load_iris(return_X_y=True)
print('Qtd. itens no conj. de treinamento:', len(iris_X))
print('Classes:', iris_y)
print('\nExemplos das medidas de 5 flores:')
print(iris_X[:5])
Qtd. itens no conj. de treinamento: 150
Classes: [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
Exemplos das medidas de 5 flores:
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]]
Aplicando o PCA na base de dados Iris
O PCA está implementado no scikit-learn e pode ser aplicado como no exemplo abaixo. Vamos criar uma função que aplica o PCA a um conjunto de dados, exibe informações de sua aplicação e retorna o conjuntos de dados transformados.
def apply_PCA(X, n_components):
pca = PCA(n_components=n_components)
new_X = pca.fit_transform(iris_X)
print('Tamanho da base de dados antes: ', X.shape)
print('Tamanho da base de dados depois: ', new_X.shape)
print('Porcentagem da variância explicada por cada coluna:', pca.explained_variance_ratio_)
print('Variância acumulada nas colunas remanescentes:', sum(pca.explained_variance_ratio_))
return new_X
Vamos aplicar o PCA nas medidas de nossas flores e observar a remoção da correlação das colunas e concentração das informações em menos colunas.
iris_X_4cp = apply_PCA(iris_X, 4)
Tamanho da base de dados antes: (150, 4)
Tamanho da base de dados depois: (150, 4)
Porcentagem da variância explicada por cada coluna: [0.92461872 0.05306648 0.01710261 0.00521218]
Variância acumulada nas colunas remanescentes: 1.0
Perceba como nossa base dados ainda possui o mesmo número de características (4). Porém, 92% da informação das colunas originais (representada pela variância) está agora concentrada na primeira coluna. Isso é um forte indicativo de que podemos classificar nossos dados utilizando menos características.
O PCA costuma ordenar as colunas da nova base de dados em ordem decrescente de quantidade de informação, então, para garantir que estamos utilizando as colunas mais informativas de nossa base, basta ignorarmos as últimas colunas da matriz.
Aplicando o PCA para 3 componentes
Agora vamos aplicar o PCA e remover a coluna menos informativa. Isso tem o mesmo efeito de utilizar as 3 primeiras colunas da matriz gerada anteriormente, mas vamos aplicar o método de novo de qualquer forma.
Repare como as colunas remanescentes ainda mantêm 99,4% da informação da base de dados original.
iris_X_3cp = apply_PCA(iris_X, 3)
Tamanho da base de dados antes: (150, 4)
Tamanho da base de dados depois: (150, 3)
Porcentagem da variância explicada por cada coluna: [0.92461872 0.05306648 0.01710261]
Variância acumulada nas colunas remanescentes: 0.9947878161267247
Vamos utilizar nossas funções de treinamento e avaliação de redes neurais para treinar um modelo nos dados reduzidos.
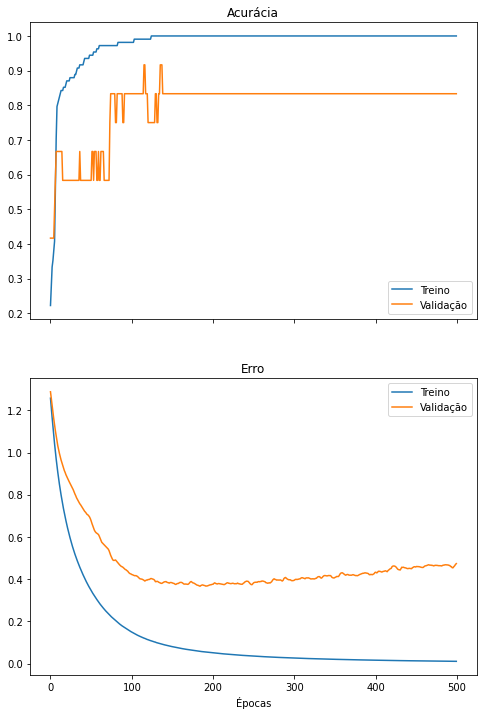
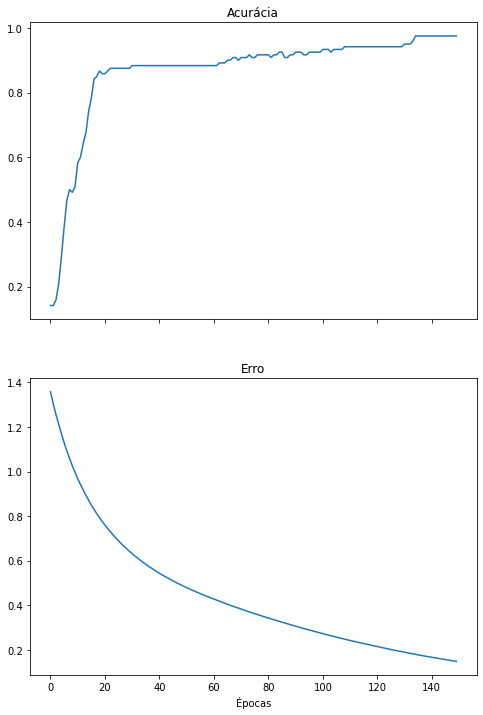
do_everything(iris_X_3cp, iris_y)
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 10) 40
_________________________________________________________________
dense_1 (Dense) (None, 8) 88
_________________________________________________________________
dense_2 (Dense) (None, 6) 54
_________________________________________________________________
dense_3 (Dense) (None, 3) 21
=================================================================
Total params: 203
Trainable params: 203
Non-trainable params: 0
_________________________________________________________________
None
precision recall f1-score support
0 1.00 1.00 1.00 13
1 1.00 1.00 1.00 6
2 1.00 1.00 1.00 11
accuracy 1.00 30
macro avg 1.00 1.00 1.00 30
weighted avg 1.00 1.00 1.00 30
[[13 0 0]
[ 0 6 0]
[ 0 0 11]]
É possível observar que a rede neural é treinada com sucesso utilizando apenas as 3 características mais informativas provenientes do PCA. A rede ainda alcança altos valores de precisão, revocação e F1-score. Também é possível perceber que, assim como no notebook anterior, o overfitting ainda ocorre caso treinemos a rede neural por épocas demais. Isso, o PCA não resolve.
Aplicando o PCA para 2 componentes
Vamos reduzir nossa base de dados mais ainda, mantendo apenas 2 colunas.
iris_X_2cp = apply_PCA(iris_X, 2)
Tamanho da base de dados antes: (150, 4)
Tamanho da base de dados depois: (150, 2)
Porcentagem da variância explicada por cada coluna: [0.92461872 0.05306648]
Variância acumulada nas colunas remanescentes: 0.977685206318795
Mesmo mantendo metade das colunas originais, ainda retemos 97,7% da informação de nossas flores. Vamos treinar nosso classificador usando esta nova base.
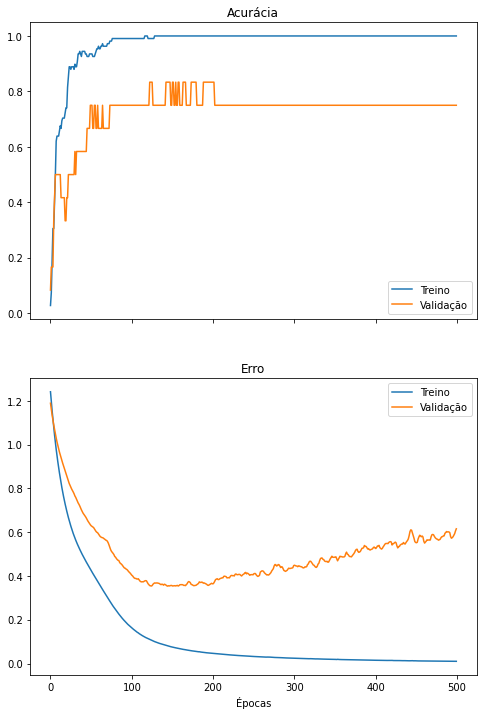
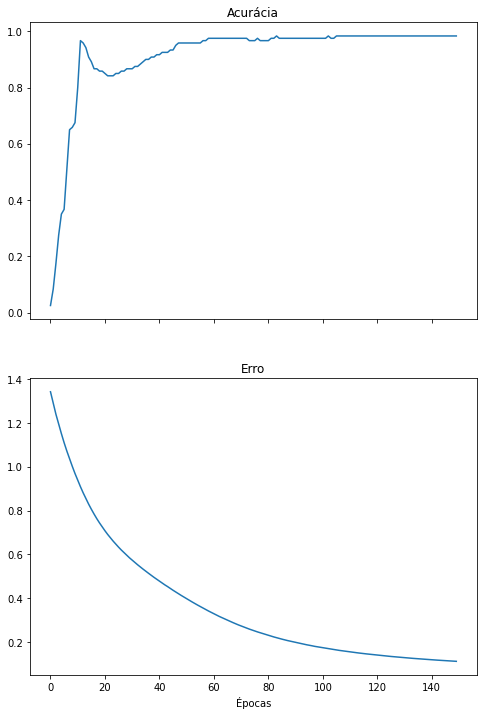
do_everything(iris_X_2cp, iris_y)
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_8 (Dense) (None, 10) 30
_________________________________________________________________
dense_9 (Dense) (None, 8) 88
_________________________________________________________________
dense_10 (Dense) (None, 6) 54
_________________________________________________________________
dense_11 (Dense) (None, 3) 21
=================================================================
Total params: 193
Trainable params: 193
Non-trainable params: 0
_________________________________________________________________
None
precision recall f1-score support
0 1.00 1.00 1.00 13
1 0.83 0.83 0.83 6
2 0.91 0.91 0.91 11
accuracy 0.93 30
macro avg 0.91 0.91 0.91 30
weighted avg 0.93 0.93 0.93 30
[[13 0 0]
[ 0 5 1]
[ 0 1 10]]
Novamente, a rede neural ainda classifica os dados com sucesso, porém pode começar a demonstrar perda de desempenho, como demonstrado por valores de precisão, revocação e F1-score menores ou uma matriz de confusão com valores fora da diagonal principal.
Outra informação muito interessante de ser reparada é a redução no número de pesos treináveis da rede, exibido no resumo da rede neural no início da célula anterior (Trainable params). A rede neural treinada para classificar os dados originais (com 4 características) precisa aprender mais pesos (213) do que uma rede que classifica dados com menos características (2 características, 193 pesos). Isso significa que, ao utilizar o PCA, uma rede neural menor que processa menos dados pode potencialmente ter o mesmo desempenho que uma rede maior que processa mais dados.
E, finalmente…
Vamos treinar a rede para classificar nossa flores utilizando apenas 1 característica. A base de dados mantém 92,4% da informação, a rede neural possui 10 pesos a menos e ainda alcança um desempenho satisfatório.
iris_X_1cp = apply_PCA(iris_X, 1)
do_everything(iris_X_1cp, iris_y)
Tamanho da base de dados antes: (150, 4)
Tamanho da base de dados depois: (150, 1)
Porcentagem da variância explicada por cada coluna: [0.92461872]
Variância acumulada nas colunas remanescentes: 0.9246187232017271
Model: "sequential_4"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_16 (Dense) (None, 10) 20
_________________________________________________________________
dense_17 (Dense) (None, 8) 88
_________________________________________________________________
dense_18 (Dense) (None, 6) 54
_________________________________________________________________
dense_19 (Dense) (None, 3) 21
=================================================================
Total params: 183
Trainable params: 183
Non-trainable params: 0
_________________________________________________________________
None
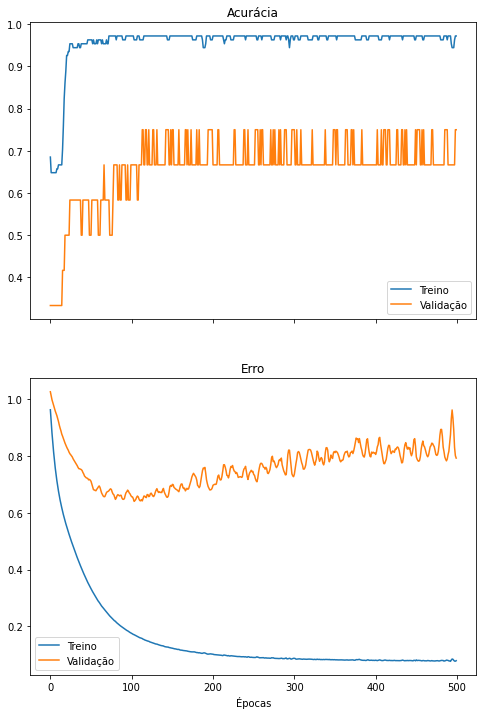
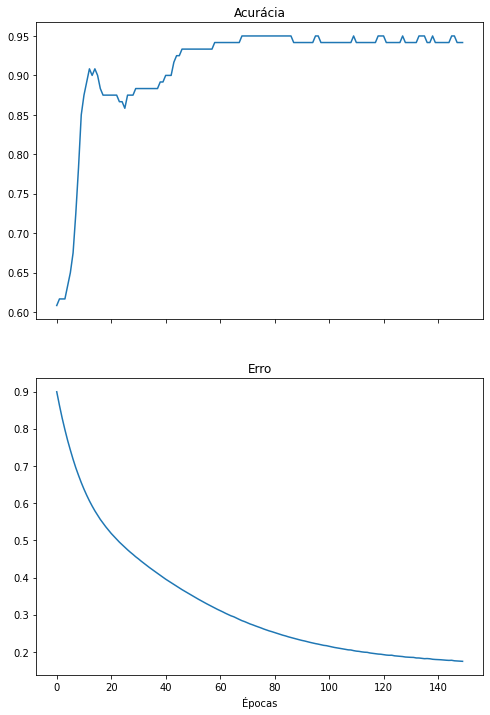
precision recall f1-score support
0 1.00 1.00 1.00 13
1 0.67 1.00 0.80 6
2 1.00 0.73 0.84 11
accuracy 0.90 30
macro avg 0.89 0.91 0.88 30
weighted avg 0.93 0.90 0.90 30
[[13 0 0]
[ 0 6 0]
[ 0 3 8]]
Conclusão
Este notebook explicou o PCA, uma técnica que transforma uma base de dados, representada por uma matriz, em uma nova matriz cujas colunas possuem menos correlação e maior concentração de informação em um menor número ce colunas.
O PCA foi exemplificado na base de dados Iris e redes neurais foram treinadas para classificar as flores utilizando cada vez menos características.
Enjoy Reading This Article?
Here are some more articles you might like to read next: